下図のような三角形ABCで、A→B→Cの順で三角形の辺をたどっていくことを考えましょう。Aから出発してもう一度Aに戻ってくるためには、1周しなければならず、合計で360度曲がらないといけません。
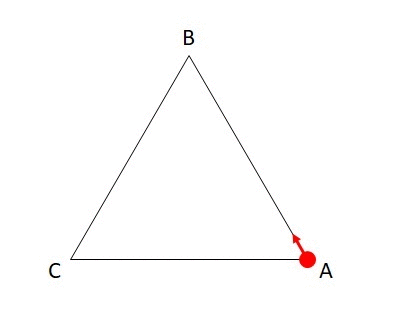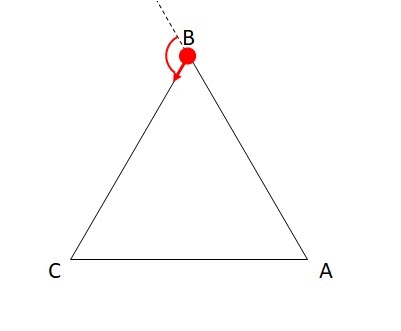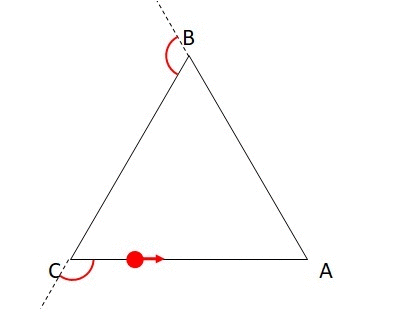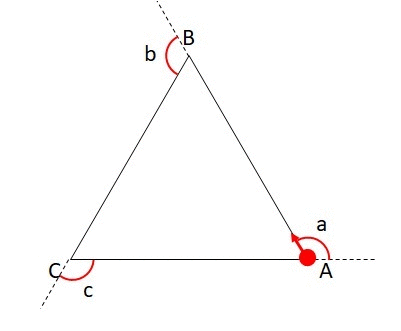
それぞれの頂点で曲がる角度をそれぞれa,b,cとすると、以下の式が成り立ちます。
\begin{equation}
a+b+c=360^\circ
\end{equation}
このa,b,cは三角形の外側の角度なので「外角」と呼ばれ、この式は「多角形の外角の和は360度になる。」という定理として中学校で習います。
さて、今求めたいのは内角の和なので、
\begin{eqnarray}
& &(180^\circ – a)+(180^\circ – b)+(180^\circ – c)\nonumber\\
&=&540^\circ – (a + b + c)\nonumber\\
&=&540^\circ – 360^\circ\nonumber\\
&=&180^\circ\nonumber
\end{eqnarray}
となり、三角形の内角の和が180度になることが導かれました。なお、2行目から3行目へは、(1)式を利用しました。
これにて、証明は終了です。本証明は、「多角形の外角の和が360度になる」ことから初めて、三角形の内角の和が180度であることを導きました。この他にも、いくつか証明方法がありますので、リンクを貼っておきます。(Quitaの証明は本記事と同様ですが、一応)
・なぜ三角形の内角の和は180度? – Qiita
・三角形の内角の和は180度って証明できるの?【三角形の外角の定理(公式)や問題アリ】
